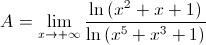Система квадратных уравнений с параметром

Рассмотрим задачу, которая может быть полезна при подготовке к ЕГЭ по математике (ЗНО з математики, ЦНТ).

Найти значения параметра   a,   при которых два квадратных уравнения имеют общий корень.

{x² + a·x + 8 = 0
{x² + x + a = 0

Предел отношения логарифмов

Найти предел отношения логарифмов  

Тригонометрическое уравнение

Рассмотрим и решим тригонометрическое уравнение

sin⁸(2·x) + cos⁸(2·x) = ⁴¹⁄₁₂₈

Иррациональное уравнение с модулем

В ЕГЭ по математике представлены задачи различного уровня, в том числе и уравнения, содержащие модуль или радикал. А иногда и модуль, и радикал. Когда нам встречается иррациональное уравнение, очевидный шаг — сразу же возводить в квадрат. Однако в особых случаях (один из таких мы сейчас и разберём) следует решать «в лоб», но с умом.
Не нужно отбрасывать лишние корни, тратить время на доказательство того, что эти лишние корни уравнения не подходят, что очень полезно на экзамене, в частности на ЕГЭ, где время решения ограничено.

Решим иррациональное уравнение, содержащее модуль:   √(5 + |x − 2|) = 1 − x

Однородное дифференциальное уравнение

Рассмотрим и решим однородное дифференциальное уравнение

(x + √(x² + y²))·y′ = y

Пределы функций, приводимые к замечательным пределам

Найдём предел функции    

Дифференциальное уравнение, допускающее понижение порядка

Найти частное решение дифференциального уравнения   y″·(1 + y) = 5·(y′)², удовлетворяющее начальным условиям:   y(0) = 0;   y′(0) = 1

Дифференциальное уравнение второго порядка

Найти частное решение дифференциального уравнения второго порядка
2·(y′)² = y″·(y − 1)   при начальных условиях:   x₀ = 1;   y₀ = 2;   y₀′ = 1

Интегрирование рациональных дробей

Найти неопределённый интеграл   I = ∫(x² + 1)·dx/(x·(x² + 4))

Иррациональное уравнение с тремя радикалами

Решить иррациональное уравнение   √(2·x + 1) + √(2·x − 4) = √(8·x − 7)

Схема урн. Извлечения без возвращения

В урне 2 белых и 3 чёрных шара. Два игрока вынимают из урна поочередно шары, не возвращая их обратно. Выиграет тот, кто раньше извлечет белый шар. Найти вероятность того, что выиграет начинающий.

Сумма бесконечного степенного ряда

Найти сумму бесконечного степенного ряда  

Разрезание куба

Можно ли разрезать куб на три равных многогранника, у каждого из которых по шесть вершин?

Система уравнений с логарифмами

Решим систему уравнений с логарифмами:

{x·y² + 2·x − x² − 2·x·y = 0 {2·logₓy + logyx = 3

(1) (2)

Дифракционная решётка

Вычислить наибольший угол, на который может отклонить пучок монохроматического света дифракционная решётка, имеющая 10000 штрихов при ширине решётки 4 см. Длина волны нормально падающего на решетку света λ = 546 нм.

---

Выразим сперва входящие в задачу величины в микрометрах:
Ширина дифракционной решётки   b = 4 см = 40000 мкм
Число штрихов   N = 10000
Длина световой волны   λ = 546 нм = 0,546 мкм
Определим теперь период дифракционной решётки:
d = b/N = 40000/10000 = 4 мкм
Согласно формуле дифракционной решётки для максимума
d·sin φ = k·λ,   где
φ — угол дифракции,
k — порядок дифракционного максимума (целое число).
Из формулы дифракционной решётки   k = d·sin φ/λ
Учитывая, что   sin φ   не может превышать единицу, найдём наибольший порядок дифракционного максимума:
k ≤ d/λ = 4/0,546 ≈ 7,3 ⇒ k_max = 7
Зная наибольший порядок дифракционного максимума, найдём наибольший угол дифракции:
sin(φ_max) = k_max·λ/d = 7·0,546/4 = 0,9555 ⇒ φ_max = arcsin 0,9555 = 72,8°

---

©   http://5ballov.pp.ua/

Физика. Равноускоренное движение

Лифт в высотном доме с верхних этажей опускается без остановок вниз со скоростью 6 м/сек до 9 этажа, затем равномерно замедляется до остановки на на первом этаже.
Какова скорость лифта на 3 этаже?

Физика. Относительность движения

С высокой башни одновременно брошены 2 тела с одинаковыми по модулю начальными скоростями, равными v = 8 м/с, при этом первое тело брошено горизонтально, а второе — вертикально вверх. Чему равно расстояние между телами через одну секунду полёта?

Интегрирование тригонометрических выражений

Вычислить определённый интеграл от тригонометрического выражения



Универсальную тригонометрическую подстановку   t = tg(ˣ/₂)   в явном виде применять не будем. Внимательно прочтём условие задачи и преобразуем подынтегральную функцию по формулам тригонометрических функций двойного аргумента:

Интегрирование иррациональных выражений. Тригонометрическая подстановка

Вычислить неопределённый интеграл   I = ∫x·dx/√(x² + 2·x + 5)

Геометрия. Описанная окружность

Площадь прямоугольника равна 240 см², а длина окружности, описанной вокруг него равна 26π см. Вычислить периметр прямоугольника.

Теория вероятностей. Дискретные случайные величины

В ящике 6 яблок и 9 груш. Наудачу извлекают 3 фрукта. Найти вероятность того, что a) все фрукты яблоки б) извлечено 1 яблоко и 1 груша в) извлечено хотя бы одно яблоко

Вступительный экзамен в МГУ. Геометрия

Окружность радиуса 6 проходит через вершину В треугольника АВС и пересекает его стороны АВ и ВС в точках Е и F соответственно. Центр О окружности лежит на стороне АС. АО = 12, СО = 10, ∠ОВС = ∠ВСО + ∠ЕОА. В каком отношении прямая ВО делит отрезок EF? Найти радиус окружности, описанной около треугольника АВС.

Основное тригонометрическое тождество

Упростите выражение: cos² b + sin⁴ b + sin² b·cos² b

Уравнение с двумя радикалами

Решить уравнение:
√[√(2х + 9/4) + 3/2] ≥ x

Типовые задачи комбинаторики

Разберём несколько типовых задач по комбинаторике

В группе 53 человека.
Сколько способов выбрать из них лучшего по математике, по физкультуре, по биологии, по экономике?
При этом каждый не может быть лучшим и там и там.

Равнобокая трапеция

Как найти высоту равнобокой трапеции, если известны диагонали и 2 основания? Основания соответственно равны 17 и 23, а диагональ 25.

Возможно ли разменять пятирублёвую монету?

Доказать,что 5 рублей не размениваются на 20 монет по 5, 20 и 50 копеек.

Вступительный в МГУ. Экзамен по математике.2

Итак, готовимся дальше к поступлению в МГУ...

Найти все функции f, удовлетворяющие уравнению
f(x) + (x − 2)·f(1) + 3·f(0) = x³ + 2

Вступительный в МГУ. Экзамен по математике

Итак, школьные экзамены позади, пора и готовиться к поступлению в ВУЗы. Во многих престижных ВУЗах страны сейчас введены вступительные письменные испытания по профильным предметам, в том числе по математике на экономичком и механико-математическом факультете МГУ. Займёмся разбором некоторых задач из экзаменов прошлых лет.

ЕГЭ по обществознанию. Как писать эссе?…

Итак, следующий ЕГЭ, который предстоит школьникам России - это ЕГЭ по обществознанию. В связи с этим возникает достаточно много вопросов, как писать эссе в части С. Постараемся дать некоторые рекомендации.

Правильная пирамида. Плоскость делит высоту в отношении…

Через ребро основания правильной четырёхугольной пирамиды проведена плоскость, которая делит площадь боковой поверхности пирамиды пополам. В каком отношении, считая от вершины, проведённая плоскость делит высоту пирамиды…?

Задача на построение по геометрии

Параллельно основаниям трапеции проведите прямую, отрезок которой заключенный внутри трапеции делился бы ее диагоналями на три равные части.

ЕГЭ математика. С6. Наименьшая и наибольшая сумма

Итак, наверное это можно назвать разбор полётов… ЕГЭ по математике написали все, хотелось бы опубликовать задание С6, до которого многие, увы, даже не дошли… Итак,

---

Каждое из чисел 13, 14, 15, … , 21 умножают на каждое из чисел 1, 2, 3, … , 6. Перед каждым из получившихся произведений ставят роизвольно знак плюс или знак минус. Какую наименьшую и наибольшую сумму по модулю можно получить в итоге?

ЕГЭ по математике. С6. Решить в натуральных числах 2^m − 3^n = 1

ЕГЭ по математике не за горами, пора начинать повторять… Ну, или учиться решать С6 — чаще всего это задачи на делимость чисел. Рассмотрим одно из таких заданий

---

Найдите все пары натуральных чисел m и n, удовлетворяющих уравнению:
2^m − 3ⁿ = 1

ЕГЭ по английскому языку 2010. Готовые письмо и эссе

4 июля — следующий экзаменационный день для российских выпускников 11 класса. Один из предстоящих экзаменов — это английский язык. Будем готовиться, и всё будет отлично!

---

Обратимся к части С ЕГЭ по английскому языку. Как известно, здесь нужно написать неофициальное письмо-ответ другу и эссе на предложенную тему. Ниже вы сможете ознакомиться с готовыми письмом и эссе и ещё раз повторить все нюансы оформления или же содержания. Ну что ж, приступим.

ЕГЭ по русскому. Сочинение с выраженной проблемой и аргументами

Итак, пора писать сочинение - рассуждение в связи с активной подготовкой к ЕГЭ по русскому языку. Вашему вниманию предлагается публицистический текст и вариант готового сочинения с выделенной проблемой и аргументами. Готовьтесь, абитуриенты!

_________________________________________________________________________

Текст

Большинство людей представляет себе счастье очень конкретно: две комнаты - счастье, три - больше счастья, четыре - просто мечта. Или красивая внешность: хотя каждый знает о "не родись красивой...", однако в глубине души мы твёрдо верим, что при ином соотношении объёмов талии и бёдер наша жизнь могла бы сложиться иначе.

Желания могут исполниться. Всегда остаётся надежда если не на стройные бёдра, то хотя бы на лишнюю комнату, а если очень повезёт - то и на дом с видом на море. Но если наши дома и фигура вообще не имеют отношения к ощущению полного блаженства? Что если в каждом из нас с рождения заложена большая или меньшая способность к счастью, как музыкальный слух или математические способности?

Именно к такому выводу пришёл психолог Роберт Мак-Крей после проведённого им десятилетнего исследования, охватившего около 5000 человек. В начале и конце опыта участникам предлагалось рассказать о событиях своей жизни и дать характеристику себе самим. Улыбчивы они или угрюмы? Видят они стакан наполовину полным или наполовину пустым?

Поразительно, но степень удовлетворённости собственной жизнью была почти одинаковой в начале и в конце исследования, независимо от того, что происходило в жизни его участников. Люди радовались, огорчались, скорбели, однако по прошествии времени возвращались к исходной точке. Уровень счастья каждого человека был связан в основном с его личностью, а не с обстоятельствами жизни.

Тогда эту неуловимую постоянную решили измерить. Психолог Ричард Дэвидсон использовал специальную технологию - позитронно-эмиссионную томографию - для измерения нейронной активности мозга в разных состояниях. Оказалось, что люди от природы энергичные, энтузиасты и оптимисты имеют высокую активность определённой области коры головного мозга - левой префронтальной зоны, которая ассоциируется с положительными эмоциями. Активность этой зоны - показатель на удивление постоянный: учёные проводили измерения с промежутком до 7 лет, и уровень активности оставался прежним. Это значит, что некоторые люди буквально рождаются счастливыми. У них желания сбываются чаще, и, даже если этого не происходит, они не зацикливаются на неудачах, а находят в ситуации светлые стороны.

Но как быть тем, чья левая префронтальная зона не так активна? Обидно жить и знать, что даже хрустальный дворец на тропическом острове не принесёт тебе счастья! К чему тогда все усилия? Зачем делать карьеру и строить дома, сидеть на диете и шить наряды, если количество счастья отмерено тебе уже при рождении и не изменится ни на йоту?

(По Н. Коршуновой)

________________________________________________________________________

Сочинение-рассуждение

В данном тексте Коршунова поднимает проблему, которая наверняка волновала каждого из нас. Как относиться к окружающей действительности, если вполне возможно, что Вы не имеете физиологических признаков, которые сделают Вас счастливыми? Смириться со своей участью, быть пессимистом, или оптимистично смотреть на мир и стремиться, несмотря ни на что, к счастью?

Автор знакомит нас с научными работами таких учёных, как Роберт Мак-Крей и Ричард Дэвидсон. Мак-Крей, анализируя результаты десятилетнего исследования, пришёл к выводу, что уровень счастья человека связан с его личностью, а не с событиями жизни. Дэвидсон же с помощью специальной технологии смог установить, что чем активнее левая префронтальная зона головного мозга, тем более счастлив человек. Эти исследования показывают то, что, оказывается, человек счастлив или несчастлив от природы.

Сама Н. Коршунова конкретного мнения по данной проблеме не выражает, но призывает нас к размышлению, задавая серию вопросов в конце повествования. Однако чувствуется некоторый пессимизм автора. Она сомневается в необходимости усилий, которые, по её мнению, никак не помогут обрести счастья, и твёрдо отмечает, что каждому из нас уже отмерена доля счастья, и эту долю изменить нельзя.

Я не полностью разделяю точку зрения Н Коршуновой. По моему мнению, счастье и радость всегда можно найти в нашем мире и нужно оставаться оптимистом. "Оптимизм - религия революций", - сказал Банвиль. То есть вера в лучшее способна перевернуть и изменить всё на свете, в том числе, возможно, и наше врождённое несчастье. Также позитивно настроен и Ален Шартье, который говорил, что "пессимизм - это настроение, а оптимизм - воля". В бизнесе, например, человек, слушающий своё настроение, мало чего добьётся, а волевой человек способен на всё. Поэтому даже зная о том, что счастья в нас заложено определённое количество, мы должны оставаться оптимистами. И если мы проявим свою волю, сможем поверить в то, что человек создан для счастья, то вполне возможно, что наше желание сможет отодвинуть физиологические причины несчастья на второй план и сделать нас счастливыми.

© http://5ballov.pp.ua/

ЕГЭ по русскому языку. С1. Постановка проблемы

ЕГЭ по русскому языку в городах России уже не за горами... 31 мая, 10 00, первый обязательный экзамен для российских школьников. Если с частью А справляются многие, с частью В также не мало учеников, то вот часть С действительно представляет для большинства школьников некоторую сложность...
______________________________________________________________________

Как начинать писать сочинение?

Главное - не бояться. Прочитали текст, расслабились, успокоились и 5 минут ничего не пишем. Просто думаем, что же мы такое прочитали, о чём прочитали. Заодно и передохнёте после активной мыслительной работы. Но сильно, наверное, расслобляться не нужно. в голове всегда чёткая, логическая схема, по которой мы и будем писать сочинение-рассуждение:

Первый абзац - постановка проблемы
↓
Второй абзац - комментарий текста
↓
Третий абзац - позиция автора
↓
Четвёртый абзац - собственная точка зрения, примеры, вывод

____________________________________________________________________

Постановка проблемы

Это, без сомнения, самый сложный этам работы, потому что именно на выделенной проблеме строится весь остальной текст сочинения. Неправильно выделенная проблема приведёт к нулям практически по всем 12 критериям оценивания Вашего сочинения.

На уроках русского языка очень часто разбирают такие проблемы, как проблема нравственного выбора, проблема цели и средств её достижения, проблема бесчеловечности и жестокости войны... Однако на ЕГЭ существует не 3-5 вариантов текстов, а больше 10, поэтому нужно быть подготовленным не только к такому узкому кругу тематики публицистических текстов. Сегодня мы познакомимся с тремя проблемами, которые не так часто встречаются в текстах, но выделять их и аргументировать необходимо уметь. Ниже вы можете познакомиться с проблемами и литературными примерами, которые можно использовать при обосновании собственного мнения.


1) Проблема бережного отношения к родному языку

• Самая большая ценность народа - его язык - язык, на котором он пишет, говорит, думает.

Д.С. Лихачёв

• Статистические данные свидетельствуют, что активный словарь Пушкина - 21000 слов. Современный образованный человек должен владеть 10 - 12 тысячами слов. Наша пресса обходится 1,5 - 2 тысячами слов. Что же тогда говорить о словаре современного школьника?

• Во дни сомнений, во дни тягостных раздумий о судьбах моей Родины, - ты один мне поддержка и опора, о великий, могучий, правдивый и свободный русский язык!

И.С. Тургенев

2) Проблема бережного отношения к наследию прошлого

• В рассказе Астафьева "Видение" ярко видно, как тяжело смотреть на уничтоженное наследие предков. Герой рассказа, смотря на развалины взорванного храма, понимает, какое чудо, созданное руками человека, было уничтожено.

• Родина подобна огромному дереву, на котором не сосчитать листьев. И всё, что мы делаем доброго, прибавляет ему силы. Но всякое дерево имеет корни. Без корней его повалил бы даже несильный ветер. Корни питают дерево, связывают его с землёй

В. Песков

• Солженицын в своём произведении "Крохотки" также обращает наше внимание на ценность культурного наследия прошлого. Звон колоколов церквей, в которые люди разных поколений вкладывали свою душу, способен возродить в сердце всё самое лучшее.


3) Проблема псевдокультуры, нравственной ответственности артиста

• В романе-эпопее Л.Н. Толстого "Война и мир" Наташа Ростова в театре прекрасно видела наигранность чувств и неприятную вычурность всех актёров, однако, следуя всеобщему мнению, начала этими артистами восхищаться. Как же можно иначе? Это же Театр...

• Публицист Л. Мозговой обращает наше внимание на нелепое словосочетание "фабрика звёзд". Настоящщие артисты не могут быть "сфабрикованы" и выпущены публике. Стать звездой - это сложная, и в первую очередь духовная работа.

• Ещё один из публицистов, Гонцов, отмечает, что сейчас многие "звёзды" с гордостью рассказывают о своём "тёмном" прошлом. Однако это не есть хороший пример для молодёжи.

Натуральные числа. Признаки делимости

Доказать, что натуральное число
a = 122333444455555666666777777788888888999999999,
десятичная запись которого состоит из одной единицы, двух двоек, трёх троек, …, девяти девяток, не может быть квадратом никакого натурального числа.

---

Рассматриваемое натуральное число содержит
N = 1 + 2 + 3 + … + 9 = 45 цифр. Но в данном случае рассматривать все цифры числа нет необходимости. Достаточно ограничиться лишь последними двумя.
Наше число — нечётное, и могло бы быть квадратом лишь нечётного числа.
Представим исходное нечётное натуральное число в виде
2·k − 1, где k — натуральное. Тогда его квадрат равен
(2·k − 1)² = 4·k² − 4·k + 1 = 4·k·(k − 1) + 1
Квадрат нечётного натурального числа при делении на 4 даёт остаток, равный только единице. Рассматриваемое же натуральное число оканчивается на 99 и при делении на 4 даёт остаток, равный 3.
Следовательно, рассматриваемое натуральное число не может быть квадратом никакого натурального числа.

---

©   http://5ballov.pp.ua/

Дифференциальное уравнение второго порядка

Найдём общее решение дифференциального уравнения второго порядка

y″ − 6·y′ + 9·y = 3·x − 8·eˣ

Дифференциальное уравнение со специальной правой частью

Найдём решение дифференциального уравнения второго порядка со специальной правой частью.

y″ − 2·y′ = e²ˣ/(1 + e²ˣ)

Планиметрия. Вписанная окружность

Задача: В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5,считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

ЕГЭ по математике. С5. Задание с параметром

И снова в ходе подготовки к ЕГЭ по математике мы обращаемся к заданию C5, которое традиционно связано с параметром. Наиболее распространённые методы его решения — это метод угловых коэффициентов и графический метод, но иногда наиболее полезной оказывается обыкновенная замена.

---

Задача
Найти все значения параметра a, при котором уравнение имеет единственное решение.

9^{х + 3·а} − 3^{х² − 4·х + 7·а} = х² − 6·х + а

Построение пятиугольника по серединам его сторон

Задача: построить пятиугольник по данным серединам его сторон.

Релятивистская квантовая физика. Эффект Комптона

Определить импульс p электрона отдачи, если фотон с энергией ε₀ = 1,53 МэВ в результате рассеяния на первоначально покоившемся свободном электроне потерял ⅓ своей энергии.

Интегрирование иррациональных выражений. Тригонометрическая подстановка

Найдём неопределённый интеграл от иррационального выражения:

I = ∫dx/(x³·√(x² − 1))

Теорія ймовірностей. Схема урн

Теория вероятностей. Схема урн

Розглянемо дві задачі з теорії ймовірностей.

Задача 1

В урне содержатся 5 белых, 3 черных и 5 красных шаров. Три шара наудачу вынимают из урны. Найти вероятность того, что хотя бы два из них будут одного цвета.

В урні містяться 5 білих, 3 чорних та 5 червоних куль. Три кулі навмання виймають з урни. Знайти ймовірніть того, що принаймні дві з куль будуть одного кольору.

Теория вероятностей. Производящая функция

Производится 4 выстрела с вероятностями попадания в цель p₁ = 0,6; p₂ = 0,4; р₃ = 0,5 и
p₄ = 0,7.

• составить закон распределения вероятностей дискретной случайной величины
  X ∈ [0; 4] — общего числа попаданий в цель;
• построить многоугольник распределения;
• найти математическое ожидание MX и дисперсию DX общего числа попаданий в цель.

ЕГЭ по математике. Задача на теорию чисел.

И вновь ЕГЭ, и вновь задание С6 по математике…
С каждым разом эти задания становятся всё страшнее и страшнее, так что даже не знаю, как сама буду чувствовать себя на экзамене… Но пока что не волнуемся, а разбираем)

Условие:
х — пятизначное натуральное число, состоящее из цифр от 1 до 9 взаимнопростое с числом В = 10⁵ − 1. Найдите количество различных чисел, включая х, взаимнопростых с В, получаемых из х циклической перестановкой цифр.

Фізика. Кінематика. Динаміка. Підготовка до ЗНО

Підготовка до ЗНО з фізики

Ядро масою m = 5 кг кидають під кутом α = 60° до горизонту, здійснюючи при цьому роботу A = 500 Дж. Нехтуючи опором повітря, визначити:

1. Через який час T ядро впаде на землю;
2. Яку відстань L по горизонталі воно пролетить.

Прийняти прискорення вільного падіння g = 10 м/с².

Интернет-олимпиада по математике. Высшая школа экономики

Разберём одно из заданий интернет-олимпиады по математике Высшей школы экономики. Это задание из курса линейной алгебры вызывало затруднения у части участников олимпиады.

---

Найти все значения параметра p, при которых найдётся не менее двух различных значений параметра q, таких, что система уравнений имеет бесконечное множество решений.

{(p − 4)·x + (p² − 7·p + 12)·y = q² − 6·q + 5
{(p − 1)·x + 8·y = 4·p·q

Диференційне рівняння першого порядку з відокремлюваними змінними

Розв'яжемо диференційне рівняння першого порядку

(2·x²·y·ln y − x)·y′ = y

ЕГЭ по математике. Теория чисел. Задача С6

Экзамены уже через 2 месяца…

Математику сдают абсолютно все одиннадцатиклассники, поэтому нужно усиленно готовиться. По-моему мнению, одной из самых сложных задач в ЕГЭ по математике является задача С6, которая посвящена теории чисел.

Предоставляю Вам решение одной из таких задач.

Найдите сумму всех трёхзначных чисел вида n, для которых n² начинается и заканчивается на цифру 1

ЕГЭ по физике. Решение задачи С3 по термодинамике

Итак, снова публикуем решение интересной задачки из ЕГЭ по физике, которая является комбинированной по темам термодинамика и закон Архимеда.

---

Имеется воздушный шар, масса оболочки которого m₁ = 400 кг. Он наполнен гелием, масса которого в свою очередь m₂ = 100 кг. Шар находится в воздухе, где температура T = 13°С и давление P = 10⁵ Па. Груз какой массы m₃ данный шар сможет удержать в воздухе?

Иррациональное уравнение

Решим иррациональное уравнение   √((x² + 4)·(x + 24)) = 5·x + 2·√(x − 1)

Фізика. Механічна система. Закон Гука. Готуємось до ЗНО

Пропоную розв'язання чергової задачі з фізики. Сподіваюсь, мої пояснення до неї допоможуть вам розв'язати цілий ряд задач і відповісти на багато тестових питань з фізики на ЗНО.

---

Вантаж деякої маси m підвішений до стелі на гумовому шнурі жорсткістю k = 250 Н/м. Якщо вантажу ударом надати швидкість, модуль якої v = 4 м/с, спрямовану вертикально вгору, то вантаж підніметься на максимальну висоту h = 90 см = 0,9 м, відраховану від його початкового положення. Визначити масу вантажу. Прискорення вільного падіння прийняти g = 10 Н/кг.

Фізика. Закон Ома. Потужність електричного струму

Фізика. Підготовка до ЗНО, ЕГЭ

Елемент з електрорушійною силою (ЕРС) E = 6 В дає максимальний струм J = 3 А (при короткому замиканні). Яка найбільша потужність Pmax може бути виділена на зовнішньому опорі?

Фізика. Електростатика. Теорема Остроградського-Гаусса

Задача
Згідно висновків квантової теорії атом гідрогену можна змоделювати у вигляді позитивного ядра (протона, розмірами якого в даній задачі можна знехтувати) та хмари негативного заряду електрона, об'ємна густина якого змінюється з відстанню від ядра за законом:
ρ(r) = −e/(π·a³) ·exp(−2·r/a), де r — відстань від центру ядра, a = 5,29·10⁻¹¹ м — радіус першої борівської орбіти в атомі гідрогену, e = 1,6·10⁻¹⁹ Кл — елементарний заряд. Знайти напруженість E електричного поля на першій борівській орбіті.

Фізика. Фотоефект. Підготовка до ЗНО, ЕГЭ

Продовжуємо публікувати цикл задач для підготовки до тестування (ЗНО, ЕГЭ), вступних випробувань та іспитів з фізики та математики.

---

Якщо почергово освітлювати поверхню металу випромінюванням з довжинами хвиль 350 нм і 540 нм, то максимальні швидкості фотоелектронів відрізнятимуться вдвічи. Визначити роботу виходу електрона для цього металу.

Фізика. Закон Кулона. Конденсатор

Плоский конденсатор електричною ємністю C = 50 мкФ з відстанню між пластинами d = 1 мм зарядили до напруги U = 220 В. Чому дорівнює сила F взаємодії між пластинами?

Система уравнений. Математика. Подготовка к ЗНО, ЕГЭ

Найти наибольшее значение x + y, где (x, y) — решение системы.

{x² – 2xy + y² = xy + 1
{x – y = 2

Питерская интернет-олимпиада по математике

Разберём одно из заданий второго тура Питерской интернет-олимпиады по математике.

Решить неравенство

Областная контрольная по физике. Разбор

Итак, за моей спиной областная контрольная по физике и по-моему написана она мною очень даже неплохо))) Не знаю, как в остальных школах, но у нас за 1 час предоставленного времени нужно было решить 111 заданий! Многовато, не так ли? Но скорее всего это была лишь ошибка разработчиков. На Ваше обозрение представляю 10 заданий из первой половины теста.
Стоит отметить, что все задания соответствуют вариантам ЕГЭ по физике, и если Вы подробно разберёте предоставленные на данном сайте решения, то это будет очень неплохой подготовкой к экзамену)) Удачи!

Диференційне рівняння, що зводиться до однорідного з відокремлюваними змінними

Розвяжемо диференційне рівняння

y′ = dy/dx = 2·((y + 2)/(y + x − 1))²

Областная контрольная по физике. Подготовка к ЕГЭ

11-12 марта в Свердловской области запланировано проведение областной контрольной по физике среди 11 классов в формате интернет-тестирования. Как обычно, учителя волнуются, ученикам как-то вообще неважно, какими будут их результаты… В общем, как обычно))

Інтегрування раціональних виразів. Тригонометрична підстановка

Знайдемо невизначений інтеграл від раціонального дробу

I = ∫dx/(x² – 2·x + 17)²

Фізика. Закон Ома. Потужність постійного струму

В нагрівачі, підключеному до акумулятора з ЕРС 12 В і внутрішнім опором 0,2 Ом, виділяється теплова потужність, яка дорівнює 100 Вт. При цьому ККД акумулятора більший за 50%. Колі спіраль перегоріла, до акумулятора підключили частину спіралі, що залишилася цілою (f = 0,8).
У скільки разів зміниться при цьому потужність в нагрівачі та ККД акумулятора?

Задача з фізики. Механіка. Динаміка. Рух по похилій площині

Тіло, сила тяжіння якого P = 1 кН, лежить на похилій шорсткій площині, нахиленій під кутом α = 30° до горизонту. Коефіцієнт тертя ковзання f = 0,1. Яку найменшу силу F потрібно прикласти до тіла, щоб протягнути його вгору по площині?

Система алгебраїчних рівнянь. Математика. Підготовка до ЗНО

Розв'яжемо систему рівнянь

{x³ + y³ = 26
{x²·y + x·y² = −6

Физика. Подготовка к ЕГЭ. Волновая оптика.

Публикуем ещё одно сообщение, которое поможет школьникам, а точнее выпускникам, качественно подготовиться к ЕГЭ (Россия) или ЗНО (Украина).
Сегодня мы опубликуем некоторые задания по волновой оптике, в которых необходимо из четырёх предложенных вариантов ответа выбрать единственный верный. Приступим.

Физика. Электростатика. Закон Кулона

Задача

Два одинаково заряженных шарика массой по 0,5 грамма, подвешенные на нитях длиною по 1м, закреплённые в одной точке, разошлись на 4 см друг от друга. Найти заряды шариков.

Интегрирование иррациональных выражений

Найдём неопределённый интеграл от иррационального выражения

Дифференциальное уравнение первого порядка

Решим дифференциальное уравнение первого порядка

6·x·dx − 6·y·dy = 2·x²·y·dy − 3·x·y²·dx

Сила упругости

Артист цирка массой m = 60 кг падает в натянутую сетку с высоты h = 4 м. С какой силой действует на артиста сетка если она прогибается при этом на x = 1 м? Ускорение свободного падения g = 9,8 м/с².

Физика. Закон сохранения энергии

Тело начинает двигаться вверх по наклонной плоскости со скоростью v₀ = 10 м/с. На высоте h = 1 м оно упруго ударяется о преграду. Определить скорость тела в момент, когда оно вновь окажется у основания наклонной плоскости. Угол наклона плоскости к горизонту α = 30°, коэффициент трения f = 0,3.

ЕГЭ математика. Диагностическая работа №3

И вот вновь в школах России должна была пройти диагностическая работа по математике в форме ЕГЭ. Точно не уверена по поводу ВСЕХ школ России, но в городе Екатеринбурге в моей школе по крайней мере, все 11-классники эту работу написали.
Как обычно, часть В у моих одноклассников и меня затруднения не вызвала.

Интегрирование тригонометрических выражений

Найдём неопределённый интеграл

Золотое руно. Литературные герои 7-8 классы

Итак, вновь обратимся к заданиям заочной гуманитарной олимпиады "Золотое руно"!!


Уважаемые участники «Золотого руна»!!! Все вопросы и стоящие предложения вы можете задавать в письменном виде на странице "Связь с нами".

А так же теперь открыта специальная тема http://5ballov.2x2forum.com/forum-f8/ на форуме, чтобы все мы вместе смогли обсудить задания из Золотого руна!!!

http://5ballov.2x2forum.com/forum.htm

Разбор заданий «Золотое руно» 9-11 класс

Уважаемые участники «Золотого руна»!!! Все вопросы и стоящие предложения вы можете оформлять и отправлять нам в письменном виде в категории сайта «Связь с нами»
 Конечно же ответы узнать можно!!! Пишите и мы договоримся с Вами!!

И ещё, ребята!!! Если уж пишете комментарии с просьбами, то оставляйте свои контакты для связи.

Блок 2
Чацкий, Онегин, Печорин
Давайте заочно познакомимся с некоторыми мужскими образами классической русской литературы. Стоит заметить, что судьбу именно этих трёх литературных героев стоит знать и помнить — как говорится, это классика жанра. А если хотите проверить себя на знание истории судьбы Чацкого, Онегина или Печорина, то попробуйте самостоятельно ответить на следующие вопросы:

Дифференциальное уравнение

Найдём общее решение дифференциального уравнения

y·y″ + (y′)² = 0

Данное дифференциальное уравнение можно решить минимум двумя способами.

Олимпиада «Золотое руно» 9-11 классы

Блок 1 — истории о трагической любви…
Каждый из нас знаком с этим прекрасным чувством — любовь… Обратимся к классической зарубежной литературе и рассмотрим некоторые всем известные истории о трагической любви и некоторые вопросы по данным произведениям…


Варианты вопросов по произведениям:

1. Трагическая история этих влюблённых — отражение реальных событий, произошедших в стенах старинного замка в конце XIII века. — Паоло и Франческа
2. «В ночи влюблённых голоса серебряною музыкой сладчайшею звучат». О каких героях идёт речь? — Ромео и Джульетта
3. Страстная любовь, овладевшая их сердцами, возникла не без помощи приворотного зелья. — Тристан и Изольда
4. «Я родилась над теми берегами, где волны как усталого гонца, встречают По с попутными реками». С какими влюблёнными связаны эти строки? — Паоло и Франческа
5. Их история была неоднократно отражена в средневековых рыцарских романах. — Тристан и Изольда
6. Знаменитый балет С. С. Прокофьева посвящён именно этим героям — балет «Ромео и Джульетта»
7. По легенде, на могилах этих влюблённых выросли деревья, которые весной переплелись ветвями — Тристан и Изольда
   

Задание по математике из олимпиады МФТИ

Решить систему уравнений:
{3x² − 2y² + 12z − 15y = 94
{2x² + z² − 20y = 34
{2x² − y² − 14x − 5y = −50
Решение:
С первого взгляда система выглядит очень страшно и даже непонятно, с какой стороны к ней можно подойти. 

Но не будем пугаться и сложим второе и третье уравнения системы:

Предел функции

Вычислим предел   .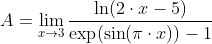
Имеем неопределённость вида   [0/0]. Приме́ним к числителю и знаменателю свойства второго замечательного предела.

Делимость целых чисел

Задача
При каких целых n число 3·n⁴ − 8·n² − 3 будет простым? Найти это простое число.

Решение:

• Разложим данный многочлен на множители:
  3·n⁴ − 8·n² − 3 = 3·n⁴ − 9·n² + n² − 3 =
  = 3·n²·(n² − 3) + n² − 3 = (n² − 3)·(3·n² +1)
• Произведение может быть простым числом только при таких целых n, при которых одна скобка равна 1, в то время как вторая является простым числом.
• Уравнение n² − 3 = 1 имеет решения n = ±2,
  при этом 3·n² + 1 = 13.
• При 3·n² + 1 = 1, получается, что n = 0. Но тогда данное число равно −3 — не простое.

Ответ:   13 при n = ±2

За грамотным выполнением контрольных работ без посредников и плагиата обращайтесь.
Звоните прямо сейчас 2427176 (Киев), (067)7384545

Предел функции. Раскрытие неопределённости

Найдём предел

Имеет место неопределённость вида 0/0.
Преобразуем числитель:

Интегрирование иррациональных выражений (тригонометрическая подстановка)

Найдём неопределённый интеграл

I = ∫√(x² + 9)·dx/x

Это интеграл от иррациональной функции. Покажем, как найти его с помощью тригонометрической подстановки.