Планиметрия. Вписанная окружность

Задача: В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5,считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

---

Решение:
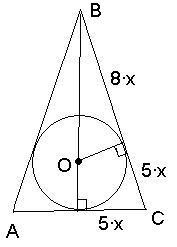Посмотрим на рисунок. Известно, что отрезки касательных равны, а радиус окружности перпендикулярен касательной, проведённой к окружности.

Пусть отрезок ВО равен у. Тогда по теореме Пифагора мы можем записать:

у² = 10² + (8·х)²

С другой стороны, также по теореме Пифагора можно записать:

(10 + у)² + (5·х)² = (5·х + 8·х)²
(10 + у)² + 25·х² = 169·х²
(10 + у)² = 144·х²
10 + у = 12·х
у = 12·х − 10

Подставим в первое квадратное уравнение значение у:

(12·х − 10)² = 100 + 64·х²
(6·х − 5)² = 25 + 16·х²
36·х² − 60·х + 25 = 25 + 16·х²
20·х² − 60·х = 0
20·х = 60
х = 3

Основание равнобедренного треугольника равно 2·5·х, и равно 30.

Ответ: 30