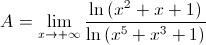
Имеет место неопределённость вида [∞/∞]. Возникает соблазн применить правило Лопиталя. Без этого метода можно обойтись, вспомнив и применив свойства логарифмической функции. Вынесем за скобки старшие члены в аргументах логарифмов и воспользуемся свойством логарифма произведения и логарифма степени:
ln(x² + x + 1) = ln(x²·(1 + 1/x + 1/x²)) = ln(x²) + ln(1 + 1/x + 1/x²) =
= 2·ln x + ln(1 + 1/x + 1/x²)
ln(x⁵ + x³ + 1) = ln(x⁵·(1 + 1/x² + 1/x⁵)) = ln(x⁵) + ln(1 + 1/x² + 1/x⁵) =
= 5·ln x + ln(1 + 1/x² + 1/x⁵)
Тогда

Учитывая, что вторые слагаемые в числителе и знаменателе последнего отношения стремятся к нулю, получим:
правило Лопиталя, свойства логарифмов, предел, неопределённость, математика, математический анализ, предел функции, контрольная по математике

Комментариев нет:
Отправить комментарий