
Начнём с определения области сходимости ряда.
Общий член исследуемого степенного ряда выражается формулой:
aռ = xⁿ/(n·(n + 1)) = bռ·xⁿ, где bռ = 1/(n·(n + 1))
Радиус сходимости ряда найдём с помощью радикального признака Коши:
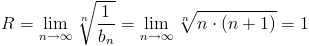
|x| < 1 — интервал сходимости ряда. На концах интервала (при x = ±1) ряд сходится абсолютно одновременно с рядом Дирихле 1/n² согласно признаку сравнения Вейерштрасса.
|x| ≤ 1 — область сходимости исследуемого ряда.
Перейдём теперь к вычислению суммы ряда.
Разложим дробь в сумму элементарных дробей:
xⁿ/(n·(n + 1)) = xⁿ/n − xⁿ/(n + 1) = xⁿ/n − ¹/ₓ · xⁿ⁺¹/(n + 1)
Тогда

Cумму S₁ найдём следующим образом: продифференцируем ряд почленно, просуммируем, а затем проинтегрируем в пределах от 0 до x.

При нахождении суммы использована формула суммы сходящейся геометрической прогрессии.
Проинтегрируем теперь в пределах от 0 до x:
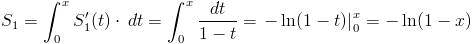
Получим: S = 1 + (x − 1)·S₁/x = 1 + (1 − x)·ln(1 − x)/x
Найденная функция имеет 2 особых точки в области сходимости исследуемого ряда.
При x → 0 получаем неопределённость вида [0/0]; при x → 1₋ — получаем неопределённость вида [0·∞]. Найдём пределы функции в этих точках.

При нахождении пределов применено правило Лопиталя.
Для проверки вычислим сумму ряда при x = 1 непосредственно:

Окончательно: S = 1 + (1 − x)·ln(1 − x)/x
Комментариев нет:
Отправить комментарий