суббота, 26 ноября 2011 г.
четверг, 24 ноября 2011 г.
Делимость суммы ряда. Олимпиадная задача
Доказать, что сумма S = 2·2 + 3·2² + 4·2³ + … + 2012·2²⁰¹¹ делится на 2011.
понедельник, 21 ноября 2011 г.
Тригонометрическое тождество
Доказать тригонометрическое тождество
sin 8°·sin 50°·sin 58° = sin 18°·sin 24°·sin 46°
sin 8°·sin 50°·sin 58° = sin 18°·sin 24°·sin 46°
пятница, 18 ноября 2011 г.
Алгебра. Система иррациональных уравнений
Найдём решения системы иррациональных уравнений
{√(x + y) − √(2·y − 5·x) = x
{√(x + y) + √(2·y − 5·x) = y
{√(x + y) − √(2·y − 5·x) = x
{√(x + y) + √(2·y − 5·x) = y
суббота, 12 ноября 2011 г.
Решение дифференциальных уравнений высших порядков
Рассмотрим на двух примерах решение дифференциальных уравнений высших порядков.
Проинтегрировать дифференциальное уравнение второго порядка
2·y·y'' – (y')² + y² = 0 при начальных условиях y(1) = y'(1) = 1
Проинтегрировать дифференциальное уравнение второго порядка
2·y·y'' – (y')² + y² = 0 при начальных условиях y(1) = y'(1) = 1
пятница, 11 ноября 2011 г.
Иррациональное уравнение с радикалами
Рассмотрим решение иррационального уравнения с радикалами
∛(x − 1) + ∛(x + 1) = x·∛2
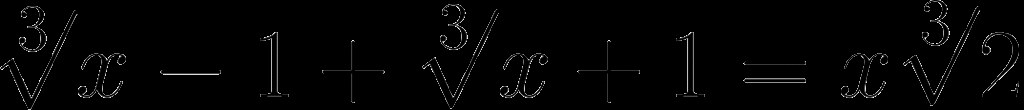
∛(x − 1) + ∛(x + 1) = x·∛2
среда, 5 октября 2011 г.
XXXIV Турнир имени М.В. Ломоносова 25 сентября 2011 года. Конкурс по математике
Дорогие ребята! 25 сентября 2011 года в городе Москва прошёл ежегодный турнир по математике имени Ломоносова. Ребята, начиная с 6 класса, решали задачи по физике, химии, математике, писали развёрнутые ответы по астрономии, истории, биологии... 5 часов в различных корпусах МГУ ребята старались показать все свои знания. В данной записи мы рассмотрим задания и решения задач по математике, ведь наверняка многим интересно, верно они решили ту или иную задачу. В скобках после номера задачи указываются рекомендуеммые классы.
четверг, 16 июня 2011 г.
Прямые в пространстве
Задача по аналитической геометрии
Составить каноническое уравнение прямой, проходящей через точку A(−6; −1; −3) и пересекающей прямую (x − 22)/5 = (y + 1)/(−1) = (z + 73)/(−18) под прямым углом.среда, 8 июня 2011 г.
Движение тел под действием силы тяжести
Продолжаем готовиться в ЕГЭ, ЗНО, ЦТ и вступительным экзаменам по физике. В этот раз мы с Вами разберём задачу на движение тела под действием силы тяжести.
Из одного положения вертикально вверх брошены друг за другом с одинаковой начальной скоростью два шарика. Второй шарик брошен в момент достижения первым максимальной высоты, равной 10 м. На какой высоте они встретятся?
Из одного положения вертикально вверх брошены друг за другом с одинаковой начальной скоростью два шарика. Второй шарик брошен в момент достижения первым максимальной высоты, равной 10 м. На какой высоте они встретятся?
вторник, 7 июня 2011 г.
Закон сохранения момента импульса
Разберём решение задачи по физике на закон сохранения момента импульса. Подобная задача может встретиться и в курсе теоретической механики, раздел Динамика.
суббота, 4 июня 2011 г.
Квадратное неравенство с параметром (задание С5 ЕГЭ)
6 июня 2011 года будет проходить Единый Государственный Экзамен (ЕГЭ) по математике.
Предлагаю Вам познакомиться с одной из вызывающих затруднения задач — квадратным неравенством с параметром.
Задание.
Найдите все значения параметра a, при каждом из которых любое решение неравенства
a·x² + (1 − a²)·x − a > 0 принадлежит отрезку [−2; 2].
Предлагаю Вам познакомиться с одной из вызывающих затруднения задач — квадратным неравенством с параметром.
Задание.
Найдите все значения параметра a, при каждом из которых любое решение неравенства
a·x² + (1 − a²)·x − a > 0 принадлежит отрезку [−2; 2].
пятница, 3 июня 2011 г.
Сходимость несобственных интегралов
Рассмотрим несколько примеров на сходимость несобственных интегралов. Как показывает опыт, в этой теме часто допускают ошибки не только студенты, но и сами преподаватели. Даже на интернет-ресурсах, позиционирующих себя как математические, подсказки даются противоречивые и зачастую — неверные.
понедельник, 25 апреля 2011 г.
Интегрирование рациональных тригонометрических функций
Найдём неопределённый интеграл от рациональной тригонометрической функции
I = ∫(4·tg x − 5)·dx/(4·cos²x − sin(2·x) + 1)
I = ∫(4·tg x − 5)·dx/(4·cos²x − sin(2·x) + 1)
суббота, 9 апреля 2011 г.
Маркетологический опрос
Одно из основных предназначений маркетинга — это помощь фирме в продвижении товара. Для того, чтобы увеличить объёмы продаж, а следовательно и прибыль, необходимо иметь чёткое представление о продвигаемой продукции. А для получения необходимой информации нужно провести исследование рынка. Очень важно определить целевую аудиторию, на которую рассчитан товар, её главные характеристики, потребности, вкусы, пожелания и т. д. Одним из наиболее распространенных методов такого исследования является опрос. Опрос должен быть небольшим, содержать наиболее важные для исследования вопросы и быть понятным для потенциальных клиентов. В данной статье приведен пример такого опроса. Приглашаем Вас в нём поучаствовать.
четверг, 3 марта 2011 г.
Покори Воробьёвы Горы — 2010. Математика. Алгебра
Дорогие школьники и абитуриенты!
Хочу предложить Вашему вниманию свой вариант решения одной из задач по алгебре заочного тура олимпиады «Покори Воробьёвы Горы» прошлого года.Условие задачи звучало следующим образом:
Найдите все значения k > 2, при каждом из которых существует непостоянная арифметическая прогрессия x₁,…, xk и квадратный трехчлен ƒ(x), для которых ƒ(x₁),..., ƒ(xk) — геометрическая прогрессия?
воскресенье, 27 февраля 2011 г.
Дифференциальное уравнение второго порядка со специальной правой частью
Найдём общее решение дифференциального уравнения второго порядка со специальной правой частью
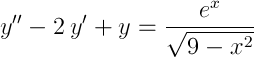
y″ − 2·y′ + y = eˣ/√(9 − x²)
четверг, 24 февраля 2011 г.
Правильный семиугольник
Разберём олимпиадную задачу по планиметрии.
Дан правильный семиугольник A₁A₂A₃A₄A₅A₆A₇. Доказать , что 1/A₁A₅ + 1/A₁A₃ = 1/A₁A₇.
Дан правильный семиугольник A₁A₂A₃A₄A₅A₆A₇. Доказать , что 1/A₁A₅ + 1/A₁A₃ = 1/A₁A₇.
воскресенье, 20 февраля 2011 г.
Золотое руно 2011. Литература
Поэзия и проза... Они прекрасны, не правда ли? Меня вдохновляет М.Ю. Лермонтов, поражает А.А. Блок, захватывает Л.Н. Толстой. Конкурс Золотое Руно вновь предоставляет задания для учеников школ, ответы на которые найти не сложно, однако сколько нового и прекрасного можно открыть для себя в глубинах Интернета! Итак, приступим.
суббота, 19 февраля 2011 г.
Золотое руно 2011. Мифология
Итак, вновь февраль, вновь приступаем к изучению Мировой Художественной Культуры, или просто МХК. Мифология, литература, наука, живопись... Это так познавательно, так интересно и несомненно заслуживает внимания школьников. Бусь ответы найдены в глубинах Рунета, но хотя бы что-то каждый участник для себя откроет и найдёт. В добрый путь и удачи в Олимпиаде!
Дальнейший материал подскажет ответы или даст возможность "свериться". Но лично от себя советую - поучитель пользоваться Google. Это совсем несложно! А заодно - подписывайтесь на обновления сайта, на котором Вам чудом удалосб оказаться. В будущем многое из его содержимого Вам будет полезно.
Дальнейший материал подскажет ответы или даст возможность "свериться". Но лично от себя советую - поучитель пользоваться Google. Это совсем несложно! А заодно - подписывайтесь на обновления сайта, на котором Вам чудом удалосб оказаться. В будущем многое из его содержимого Вам будет полезно.
понедельник, 31 января 2011 г.
Дифференциальное уравнение третьего порядка
Найдём общее решение дифференциального уравнения третьего порядка со специальной правой частью
вторник, 11 января 2011 г.
Покори Воробьёвы Горы – 2011. Физика. «Магнитный удар»
Дорогие школьники!
Сегодня я подготовил для вас подарок — подробное решение 3-й задачи заочного тура олимпиады по физике. Сложность этой задачи в том, что она — комплексная: требует применения знаний из кинематики, динамики, электродинамики, геометрии… Пожалуйста, используйте материалы сайта с умом: не переписывайте решения дословно. Вы должны понимать, что несколько идентичных работ не получат положительные оценки от жюри олимпиады. Если возникнут сложности с подготовкой к очному туру олимпиады — обращайтесь ко мне через форму обратной связи на сайте.И не забывайте, что согласно Регламенту проведения Олимпиады работы должны быть отправлены до 15 января 2011 года (до 24.00 часов по московскому времени). В этом году сроки отправки работ продлеваться не будут.
«Магнитный удар»
Из верхней точки закрепленного вертикально проводящего кольца радиуса R падает без начальной скорости маленькое тело. В момент пролета телом центра кольца через кольцо пропускают заряд величиной Q (время прохождения заряда много меньше времени падения тела). В результате тело отклонилось от вертикали и его соударение с кольцом произошло не в нижней точке кольца, а на высоте h ≪ R. Найти удельный заряд тела (то есть отношение заряда к массе).
Перейдём к решению задачи
понедельник, 10 января 2011 г.
Физика «ПОКОРИ ВОРОБЬЁВЫ ГОРЫ – 2011!». Заочный тур
ОЛИМПИАДА ШКОЛЬНИКОВ
«ПОКОРИ ВОРОБЬЁВЫ ГОРЫ – 2011!»
Заочный тур
ФИЗИКА. 11 класс
Седьмой год подряд Московский университет им. М. В. Ломоносова совместно с газетой «Московский комсомолец» проводит олимпиаду «ПОКОРИ ВОРОБЬЕВЫ ГОРЫ!» для школьников изо всех без исключения уголков России. Огромная заслуга в развитии олимпиадного движения и приумножении добрых традиций российского образования принадлежит ректору МГУ имени М. В. Ломоносова академику Виктору Садовничему и главному редактору газеты «Московский комсомолец» Павлу Гусеву.
Подписаться на:
Сообщения (Atom)