Иррациональное уравнение с радикалами

Рассмотрим решение иррационального уравнения с радикалами

∛(x − 1) + ∛(x + 1) = x·∛2

Возведём обе части уравнения в куб. Поскольку мы возводим в нечётную степень, корни уравнения не потеряются и лишние корни не появятся.

x − 1 + x + 1 + 3·∛((x − 1)·(x + 1))·(∛(x − 1) + ∛(x + 1)) = 2·x³

Приведём подобные слагаемые. Сумму радикалов в скобках заменим на правую часть исходного уравнения.

2·x + 3·x·∛(2·(x² − 1)) = 2·x³

Сгруппируем теперь все слагаемые в левой части уравнения.

2·x³ − 2·x − 3·x·∛(2·(x² − 1)) = x·(2·(x² − 1) − 3·∛(2·(x² − 1))) = 0

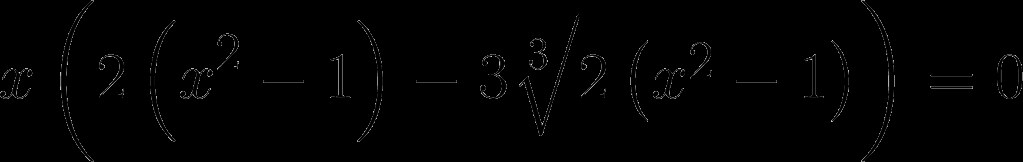
Один из корней уравнения очевиден:   x₁ = 0. Найдём остальные корни.

2·(x² − 1) − 3·∛(2·(x² − 1)) = ∛(2·(x² − 1))·(∛(2·(x² − 1))² − 3) = 0

x² − 1 = 0 ⇒ x₂₃ = ±1

∛(2·(x² − 1))² = 3 ⇒ 2·(x² − 1) = ±3^3/2 = ±3·√3 ≥ −2

2·(x² − 1) = +3·√3 ⇒ x² − 1 = ³⁄₂ √3 ⇒ x² = 1 + ³⁄₂ √3

x₄₅ = ±√(1 + ³⁄₂ √3)

Ответ:   x = {0; ±1; ±√(1 + ³⁄₂ √3)}. Всего 5 действительных корней.

Именно проявив аккуратность, мы не потеряли ни единого корня уравнения. Будьте внимательны при решении математических задач. Всем успехов в учёбе!

---

©   http://5ballov.pp.ua/