Найдём общее решение дифференциального уравнения второго порядка со специальной правой частью
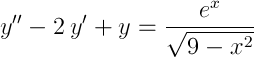
Это дифференциальное уравнение может быть решено методом вариации произвольной постоянной. Но существует и другой, более простой, способ. Разберём оба способа решения.
Характеристическое уравнение k² − 2·k + 1 = (k − 1)² = 0 имеет двухкратный действительный корень k₁ = k₂ = 1, откуда одно из общих решений соответствующего однородного дифференциального уравнения (с точностью до постоянной интерирования) y₀ = eˣ.
Домножим обе части исходного дифференциального уравнения на e⁻ˣ:
(y″ − 2·y′ + y)·e⁻ˣ = 1/√(9 − x²)
В левой части последнего уравнения — вторая производная произведения y·e⁻ˣ. Покажем это, применив формулу Лейбница:
(y·e⁻ˣ)″ = y″·e⁻ˣ + 2·y′·(e⁻ˣ)′ + y·(e⁻ˣ)″ = (y″ − 2·y′ + y)·e⁻ˣ
Таким образом, дифференциальное уравнение перепишется в виде:
(y·e⁻ˣ)″ = 1/√(9 − x²)
Проинтегрируем дважды.
(y·e⁻ˣ)′ = ∫dx/√(9 − x²) = ∫d(ˣ⁄₃)/√(1 − (ˣ⁄₃)²) = arcsin(ˣ⁄₃) + C₁
y·e⁻ˣ = ∫(arcsin(ˣ⁄₃) + C₁)·dx = [интегрирование по частям] = x·arcsin(ˣ⁄₃) + C₁·x −
− ∫x·d(arcsin(ˣ⁄₃)) = x·arcsin(ˣ⁄₃) + C₁·x − ∫x·dx/√(9 − x²) = x·arcsin(ˣ⁄₃) + C₁·x +
+ ½ ∫d(9 − x²)/√(9 − x²) = x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂
Домножая на eˣ, получим общее решение дифференциального уравнения:
y = (x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂)·eˣ
Найдём теперь решение уравнения методом вариации произвольной постоянной.
Корни характеристического уравнения k₁ = k₂ = 1.
Однородное дифференциальное уравнение имеет два линейно независимых решения:
y₁ = x·eˣ, y₂ = eˣ ⇒ y₁ = x·y₂ = x·eˣ
Общее решение неоднородного дифференциального уравнения будем искать в виде:
y = C₁(x)·y₁ + C₂(x)·y₂ = (C₁(x)·x + C₂(x))·y₂ = (C₁(x)·x + C₂(x))·eˣ,
где C₁(x), C₂(x) — неизвестные функции, которые определяются из системы уравнений
{C₁′(x)·y₁ + C₂′(x)·y₂ = 0
{C₁′(x)·y₁′ + C₂′(x)·y₂′ = eˣ/√(9 − x²)
Дифференцируем: y₁′ = (x + 1)·eˣ, y₂′ = eˣ.
Подставляя производные в систему уравнений, получим:
{x·C₁′(x)·eˣ + C₂′(x)·eˣ = 0
{(x + 1)·C₁′(x)·eˣ + C₂′(x)·eˣ = eˣ/√(9 − x²)
⇓
Проинтегрируем, опуская приведенные выше выкладки.
C₁(x) = ∫dx/√(9 − x²) = arcsin(ˣ⁄₃) + C₁; C₂(x) = −∫x·dx/√(9 − x²) = √(9 − x²) + C₂
Общее решение дифференциального уравнения:
y = (x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂)·eˣ

y″ − 2·y′ + y = eˣ/√(9 − x²)
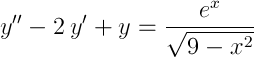
Это дифференциальное уравнение может быть решено методом вариации произвольной постоянной. Но существует и другой, более простой, способ. Разберём оба способа решения.
Характеристическое уравнение k² − 2·k + 1 = (k − 1)² = 0 имеет двухкратный действительный корень k₁ = k₂ = 1, откуда одно из общих решений соответствующего однородного дифференциального уравнения (с точностью до постоянной интерирования) y₀ = eˣ.
Домножим обе части исходного дифференциального уравнения на e⁻ˣ:
(y″ − 2·y′ + y)·e⁻ˣ = 1/√(9 − x²)
В левой части последнего уравнения — вторая производная произведения y·e⁻ˣ. Покажем это, применив формулу Лейбница:
(y·e⁻ˣ)″ = y″·e⁻ˣ + 2·y′·(e⁻ˣ)′ + y·(e⁻ˣ)″ = (y″ − 2·y′ + y)·e⁻ˣ
Таким образом, дифференциальное уравнение перепишется в виде:
(y·e⁻ˣ)″ = 1/√(9 − x²)
Проинтегрируем дважды.
(y·e⁻ˣ)′ = ∫dx/√(9 − x²) = ∫d(ˣ⁄₃)/√(1 − (ˣ⁄₃)²) = arcsin(ˣ⁄₃) + C₁
y·e⁻ˣ = ∫(arcsin(ˣ⁄₃) + C₁)·dx = [интегрирование по частям] = x·arcsin(ˣ⁄₃) + C₁·x −
− ∫x·d(arcsin(ˣ⁄₃)) = x·arcsin(ˣ⁄₃) + C₁·x − ∫x·dx/√(9 − x²) = x·arcsin(ˣ⁄₃) + C₁·x +
+ ½ ∫d(9 − x²)/√(9 − x²) = x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂
Домножая на eˣ, получим общее решение дифференциального уравнения:
y = (x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂)·eˣ
Найдём теперь решение уравнения методом вариации произвольной постоянной.
Корни характеристического уравнения k₁ = k₂ = 1.
Однородное дифференциальное уравнение имеет два линейно независимых решения:
y₁ = x·eˣ, y₂ = eˣ ⇒ y₁ = x·y₂ = x·eˣ
Общее решение неоднородного дифференциального уравнения будем искать в виде:
y = C₁(x)·y₁ + C₂(x)·y₂ = (C₁(x)·x + C₂(x))·y₂ = (C₁(x)·x + C₂(x))·eˣ,
где C₁(x), C₂(x) — неизвестные функции, которые определяются из системы уравнений
{C₁′(x)·y₁ + C₂′(x)·y₂ = 0
{C₁′(x)·y₁′ + C₂′(x)·y₂′ = eˣ/√(9 − x²)
Дифференцируем: y₁′ = (x + 1)·eˣ, y₂′ = eˣ.
Подставляя производные в систему уравнений, получим:
{x·C₁′(x)·eˣ + C₂′(x)·eˣ = 0
{(x + 1)·C₁′(x)·eˣ + C₂′(x)·eˣ = eˣ/√(9 − x²)
⇓
| {x·C₁′(x) + C₂′(x) = 0 {(x + 1)·C₁′(x) + C₂′(x) = 1/√(9 − x²) | ⇒ | {C₁′(x) = 1/√(9 − x²) {C₂′(x) = −x/√(9 − x²) |
Проинтегрируем, опуская приведенные выше выкладки.
C₁(x) = ∫dx/√(9 − x²) = arcsin(ˣ⁄₃) + C₁; C₂(x) = −∫x·dx/√(9 − x²) = √(9 − x²) + C₂
Общее решение дифференциального уравнения:
y = (x·arcsin(ˣ⁄₃) + √(9 − x²) + C₁·x + C₂)·eˣ

огромное спасибо!
ОтветитьУдалить