Правильная четырёхугольная пирамида

В правильной четырёхугольной пирамиде SABCD с вершиной S найдите тангенс угла между прямыми SA и DM, где М — середина ребра SC, AS=12, BC=3·√2

---

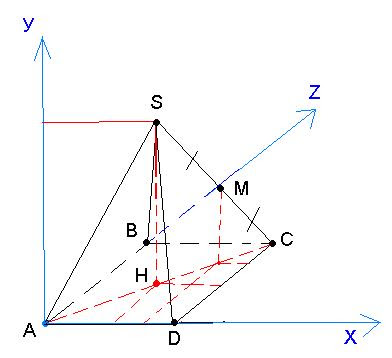
Задачу будем решать с помощью метода координат.

Совместим вершину А правильной пирамиды с началом отсчёта, а плоскость основания — с плоскостью ZOХ (см. рисунок).
Координаты точки А:




А (0; 0; 0)
Координаты точки D:

D (3·√2; 0; 0)

Чтобы найти координаты точки S, нужно найти SH и AH. Учитывая, что в правильной четырёхугольной пирамиде основание — это квадрат, по теореме Пифагора можем записать:

2·AH = √(2·(3·√2)²) = √36 = 6
 AH = 3




SH = √(12² − AH²) = √(144 − 9) = 3·√15

Так как высота в правильной пирамиде опускается в центр основания, то координаты точки S:




S (1,5·√2; 3·√15; 1,5·√2)

По обобщённой теореме Фалеса перпендикуляр, опущенный из точки М к основанию пирамиды, попадёт в центр НС. Из этого следует, что этот перпендикуляр будет равен половине SH. Запишем координаты точки М:





М ( (3/4)·3·√2; 1,5·√15; (3/4)·3·√2)
M (2,25·√2; 1,5·√15; 2,25·√2)

Теперь перейдём к векторам. Запишем координаты векторов АS и DM:

AS (1,5·√2; 3·√15; 1,5·√2)

DM (2,25·√2 − 3·√2; 1,5·√15; 2,25·√2)

DM (−0,75·√2; 1,5·√15; 2,25·√2)

Косинус угла между векторами найдём по формуле:

cos α = (AS·DM)/(|AS|·|DM|)

AS·DM = 1,5·√2·(−0,75·√2) + 3·√15·1,5·√15 + 1,5·√2·2,25·√2 =
= - 2,25 + 67,5 + 6,75 = 72

|AS|·|DM| = √(2,25·2 + 9·15 + 2,25·2)·√(0,5625·2 + 2,25·15 + 5,0625·2) =
= √(9·16)·√((18 + 540 + 162)/16) = 3·√720 = 36·√5

cos α = 72/(36·√5) = 2/√5

Известно, что:

tg² α = (1/cos² α) − 1 = 5/4 − 1 = ¼

Так как угол α между прямыми лежит в пределах от 0º до 180º, то тангенс этого угла положителен, из-за того, что положителен косинус.

tg α = 0,5

Ответ: tg α = 0,5