Предел функции

Вычислим предел   .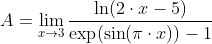
Имеем неопределённость вида   [0/0]. Приме́ним к числителю и знаменателю свойства второго замечательного предела.

Делимость целых чисел

Задача
При каких целых n число 3·n⁴ − 8·n² − 3 будет простым? Найти это простое число.

Решение:

• Разложим данный многочлен на множители:
  3·n⁴ − 8·n² − 3 = 3·n⁴ − 9·n² + n² − 3 =
  = 3·n²·(n² − 3) + n² − 3 = (n² − 3)·(3·n² +1)
• Произведение может быть простым числом только при таких целых n, при которых одна скобка равна 1, в то время как вторая является простым числом.
• Уравнение n² − 3 = 1 имеет решения n = ±2,
  при этом 3·n² + 1 = 13.
• При 3·n² + 1 = 1, получается, что n = 0. Но тогда данное число равно −3 — не простое.

Ответ:   13 при n = ±2

За грамотным выполнением контрольных работ без посредников и плагиата обращайтесь.
Звоните прямо сейчас 2427176 (Киев), (067)7384545

Предел функции. Раскрытие неопределённости

Найдём предел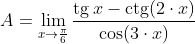

Имеет место неопределённость вида 0/0.
Преобразуем числитель:

Интегрирование иррациональных выражений (тригонометрическая подстановка)

Найдём неопределённый интеграл

I = ∫√(x² + 9)·dx/x

Это интеграл от иррациональной функции. Покажем, как найти его с помощью тригонометрической подстановки.